1.1. Системы счисления и преобразования между ними
Различные системы счисления отличаются не только базовым набором чисел, но и основными концепциями, которые лежат в их основе. Взять, например, систему счисления, которая использовалась древними римлянами: она довольно трудна для восприятия, в ней очень сложно производить вычисления и невозможно представить 0. Данная система неудобна даже для человека, не говоря уж о том, чтобы научить компьютер «понимать» ее. Десятичная система, которую мы используем всю жизнь, относится к классу так называемых позиционных систем, в которых число А может быть представлено в виде:
А = а V + а •а*"1 + ... + a,*z'+a *z°
Здесь an — это цифры числа, a Z — основание системы счисления, в нашем
случае — 10.
Например, число 1234 можно представить так:
1234 = 1*103 + 2*102 + 3*10' + 4*10°
«Вес» каждой цифры определяется позицией цифры в числе и равен степени
основания, соответствующей ее позиции.
При работе с различными системами счисления мы будем записывать само
число в скобках, а за скобками — основание системы. Например, если написать
просто число 1100, то не понятно, в какой системе оно записано — это
может быть одна тысяча сто, а может быть 12, если число записано в двоичной
системе. А если представить число в виде (1100)2, то сразу все становится на
свои места: число записано в двоичной системе. Кстати, двоичная система
тоже является позиционной, поэтому число 1100 в двоичной системе мы
можем представить так:
(1100), = 1*23 + 1*22 + 0*2' + 0*2°
После сложения 8+4 мы получим, что (1100)2 равно 12. Как видите, все точно
так же, как и с десятичной системой. Обратите внимание, что для представления
числа 12 в двоичной системе использованы только четыре разряда.
Наибольшее число, которое можно записать четырьмя двоичными цифрами,
равно 15, потому что (1Ш)2 = I*8 + I*4 + I*2 + 1*' = 15.
Давайте рассмотрим
первые 16 чисел:
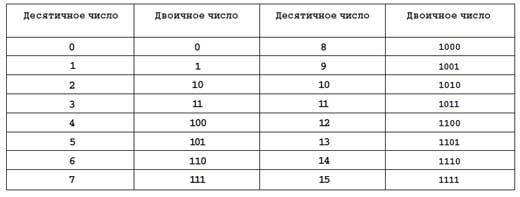
Числа растут равномерно, и нетрудно предположить, что 16 будет представлено
в двоичной системе как (10000)2.
Восьмеричная система счисления (по основанию 8) состоит из большего
количества цифр — из восьми (от 0 до 7). Преобразование из этой системы
в десятичную систему полностью аналогично преобразованию из двоичной
системы, например:
(77)8 = 7*8' + 7*8° - 63
Восьмеричная система счисления использовалась в очень популярных ранее 8-
битньгх компьютерах ATARI, ZX Spectrum и др. Позже она была заменена шест-
надцатеричной системой, которая также будет рассмотрена в этой книге.
В шестнадцатеричной системе цифрами представлены только первые 10 чисел,
а для представления остальных 5 чисел используются символы A-F:
А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15
Материал взят с книги Рудольф Марек "АССЕМБЛЕР на примерах Базовый курс"
Скачать книгу полностью
Другие новости